Vitesse et accélération dans différents systèmes de coordonnées

LES DIFFERENTS SYSTEMES DE COORDONNEES

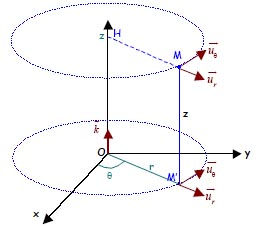
Coordonnées cylindriques

Base orthonormée directe:

Coordonnées cylindriques du point M:

Lien entre coordonnées cylinriques et coordonnées cartésinnes:

Coordonnées sphériques

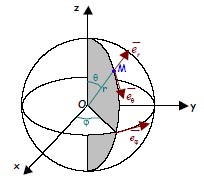
Base orthonormée directe:

Coordonnées du point M:

Lien entre coordonnées sphériques et coordonnées cartésiennes:

VITESSE ET ACCELERATION

Définition

Soit l'équation de la trajectoire.

Le vecteur vitesse est ; il est en tout point tangent à la trajectoire. Sa norme s'exprime en m/s.

Le vecteur accélération est ; il n'est a priori pas tangent à la trajectoire, mais il est toujours dirigé vers le centre de la trajectoire. Sa norme s'exprime en m/s².

Vitesse et accélération en coordonnées cartésiennes

En coordonnées cartésiennes,on a :

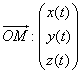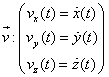trajectoire : , vitesse : , accélération : .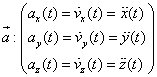

Vitesse et accélération dans le repère de Frenet

Cette base intrinsèque est constituée de deux vecteurs untaires (un vecteur tangent à la trajectoire ret un vecteur normal à la trajectroire et dirigé vers son centre de courbure): base orthonormée intrinsèque: . On note R le rayon de courbure.

vitesse: , accélération: .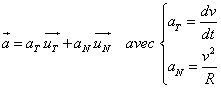

MOUVEMENT CIRCULAIRE UNIFORME

Soit n la fréquence du mouvement (en tour/seconde) et R le rayon de la trajectoire (en mètre).

La période est ; la vitesse angulaire vaut en norme (rad/s); la vitesse linéaire vaut en norme (m/s).

Coordonnées dans la base de Frenet:

vitesse: ; accélération: .